強震アレイを用いたアスペリティのイメージングに関する研究
このトピックスは、本多亮(温泉地学研究所)が青井真(防災科学技術研究所)、関口春子(産業技術総合研究所)らと共同で行った研究「強震アレイを用いた2003年十勝沖地震のアスペリティ(右下囲み記事参照)のイメージング」について、地球物理学専門誌・Geophysical Journal Internationalに掲載されたものを再編集して掲載したものです
引用文献:
R. Honda, S. Aoi, H. Sekiguchi, H. Fujiwara (2008) Imaging an asperity of the 2003 Tokachi-oki earthquake using a dense strong-motion seismograph network, Geophysical Journal International 172 (3) , 1104–1116 doi:10.1111/j.1365-246X.2007.03702.x .
研究の動機
地震とは、「地下の岩盤が急激にズレ動くこと」で、そのずれが地表面にまで達すると活断層として認識されます。しかし、岩盤のずれは断層面上で一定ではなく、たくさん滑るところもあれば、わずかしか滑らない部分もあります。アスペリティとは、断層面上で大きく滑って、強い地震波を発生させる領域のことを指します。詳しくはこちら。
この点については複数の研究者の結果が一致しています。しかし、多くの観測点、特に北海道東部(道東)の観測点では、この最大のアスペリティ以外から来たと考えられる波群が観測されており、その発生源についてははっきりとしたことが分かっていませんでした。Honda et al. (2004)の解析(図1)では、Cと書かれたアスペリティがその発生源としてやや不明瞭ながら見えています。
そこで本研究では、従来の解析手法とは違う手法を採用し、道東で観測される波群を発生させたアスペリティの位置を正確に推定しました。
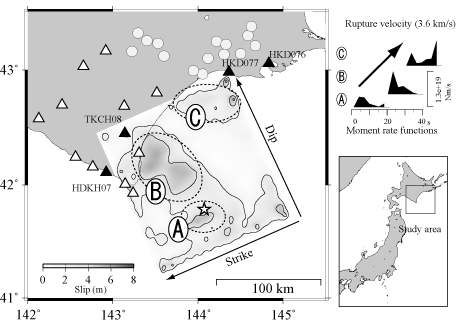
図1:従来の波形逆解析によって得られた滑り量分布図(Honda et al., 2004)
A,B,およびCの3つのアスペリティが求められた。黒と白の三角形は波形逆解析で使用した観測点。丸は本研究で使用した観測点。
解析手法
本研究では、物理探査や散乱体の研究でよく使われているセンブランス解析の手法をアスペリティ位置の推定に応用します。
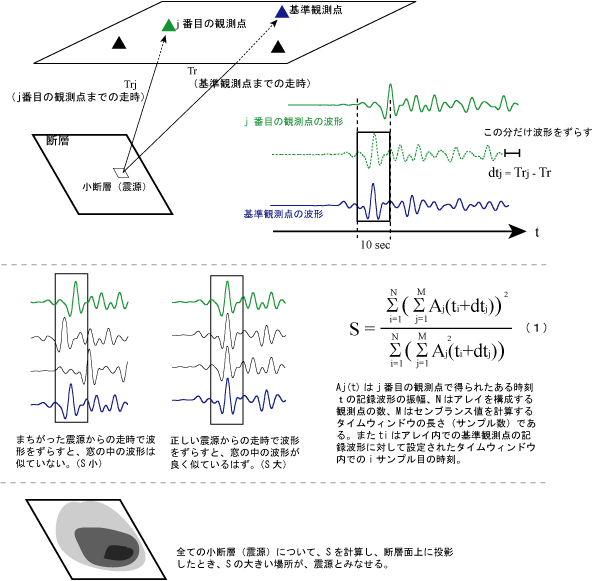
図2:センブランス解析の概念図
解析手法を図2に示します。断層面を仮定し2kmの小断層に区切ります。各小断層から各観測点までの走時(到達するまでにかかる時間)を計算し、 その時間差に応じて各観測点での観測波形の時間をずらしてセンブランス値Sを計算します。センブランス値は、おおまかには波形がどのくらい似ているか、という指標で、値が大きいほど波形が似ているといえます。ある小断層から地震波が放射されたと仮定してセンブランス値を計算し、そのセンブランス値を小断層上に投影すると、どこからその地震波が来たと考えるのが妥当か、ということが分かります。
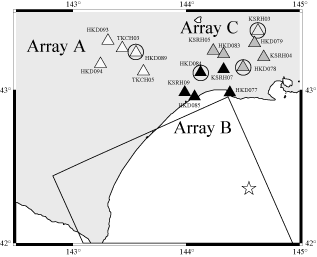
図3:観測点分布図。防災科研の強震ネット(K-NET)観測点を3つのアレイ(白、グレー、黒の三角)とみなした。
このような解析をするためには、解析したい地震波の波長に対して十分狭い範囲になるべくたくさんの観測点(観測点の集まりをアレイといいます)が必要となります。そこで、今回は道東に設置されている防災科研のK-NETの観測点を仮想的にアレイとみなして解析を行いました(図3)。
さらに、センブランス値を計算する際には、なるべく精度よく断層面から各観測点までの走時が わかっている必要があります。そこで、本震の断層面周辺で発生した余震の波形を使い、その波形が再現できるような速度構造モデルを作成し、走時計算に使います。さらに、観測点ごとのローカルな速度構造の差を考慮するため、理論走時と観測走時を比較し、その差を補正してセンブランス値を計算しました。
結果
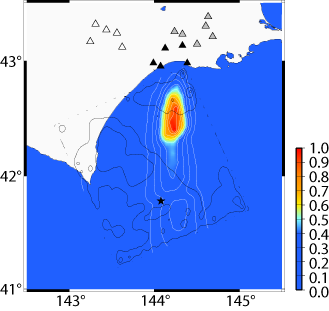
図4:推定されたアスペリティの位置
従来の手法では、道東で観測された波群の震源(アスペリティ)がはっきりと分からなかったのに対し、本研究では、はっきりとした位置が推定できました。
本研究の意義
また、理論波形の計算など時間のかかる重たい処理をする必要がないので、迅速にすべり領域の広がりなどを把握したい場合にも対応できると考えられます。
神奈川県西部地域では、以前からM7クラスの地震が発生する可能性が指摘されています。今回の解析で使用したK-NETの観測網ではM7クラスの地震を解析するには粗すぎますが、足柄平野などに展開されているSK-netなどのデータを利用すれば、そのような地震についても詳細な震源像を推定できると考えられます。
